Dr. Felice Nunziata

Il profilo aerodinamico ottimale dei proiettili

Uno dei più interessanti problemi relativi alla balistica esterna è quello della ricerca del profilo di un proiettile che risenta il meno possibile della forza di resistenza aerodinamica.

Nella fattispecie possiamo generalizzare riferendoci a quelle forze che, agendo sul proiettile, ne caratterizzano il moto relativamente al fluido interessato. Queste forze dipendono dalla velocità relativa.

Un proiettile moderno consiste, essenzialmente, di tre parti fondamentali ossia di un corpo centrale cilindrico che impegna la rigatura della canna, di un fondello e di una testa di varie ed opportune geometrie.

Innanzitutto, dovendo descrivere le forze agenti sul proiettile, si è soliti definire due importanti punti d`applicazione delle stesse.

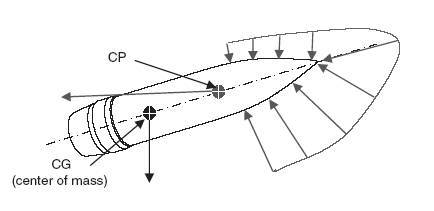
Fig.1

Il centro di massa o centro di gravità CG è il luogo geometrico nel quale può intendersi concentrata tutta la massa del proiettile e quindi applicata l`azione della forza di gravità.

Il centro di pressione o CP è, invece, il punto ove agisce la risultante delle infinitesimali forze di pressione a cui è soggetto il proiettile nel suo incedere attraverso il fluido aria.

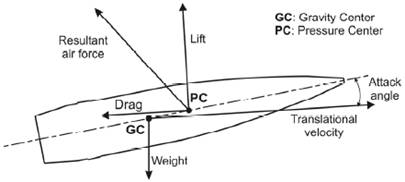
Fig.2

La posizione relativa dei due punti, ossia la successione descritta in figura o quella opposta, comporta differenti effetti stabilizzanti (cfr. fin-stabilized projectiles) o destabilizzanti (cfr. spin-stabilized projectiles) a seconda della natura, appunto, del proiettile.

La differente posizione di CP e CG comporta comunque un effetto di capovolgimento che risulta mitigabile attraverso l`induzione di un`appropriata velocità angolare o rotazionale rispetto all`asse longitudinale del proiettile mediante il tormento meccanico prodotto dal forzamento della parte cilindrica rispetto alla rigatura della canna.

Il proiettile nel momento in cui ha lasciato la canna è soggetto agli effetti indotti dalla forza di gravità, a quelli della pressione relativa dell`aria (intesa quale fluido viscoso e compressibile) ed a quelli indotti dalla rotazione rispetto al suo asse longitudinale.

Nello spazio libero il proiettile risulta a tutti gli effetti un solido di rotazione dotato di tre assi di simmetria rispetto ai quali definire coordinate e di conseguenza effetti rotazionali, quali rollio, beccheggio ed imbardata.

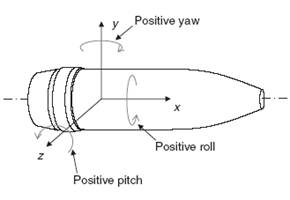
Fig.3

Lo studio e la rappresentazione del moto del proiettile nell`aria è molto complicato poiché le caratteristiche fisiche che entrano in gioco sono il numero di Reynolds, la velocità relativa rispetto a quella del suono e la viscosità cinematica. 

Le forze riportate in fig.2 ed indotte dalla presenza dell`aria sono, in un`analisi fenomenica semplificata, quelle maggiormente rappresentative: infatti, la drag force è da intendersi quella di resistenza aerodinamica mentre la lift force è interpretabile come una forza di spinta aerodinamica.

Quest`ultima, risulta crearsi in virtù dell`effetto Bernoulli che si manifesta quando i filetti fluidi investono asimmetricamente un corpo in moto relativo, creando una distribuzione (asimmetrica) delle pressioni (e quindi delle velocità del fluido prossimo al profilo del corpo), fenomeno analogo a quello che permette alle ali di un aereo di creare portanza quindi decollare e volare.

Viceversa la drag force rappresenta, in questo modello semplificato, l`effetto della resistenza dell`aria all`incedere del proiettile.

Gli effetti della drag force sono descrivibili in funzione della velocità relativa del proiettile e quindi come indicatore dei fenomeni relativi ci si riferisce ad un indicatore sinottico che èdato dal numero di Reynolds: infatti, quest`ultimo essendo un indicatore della viscosità cinematica dell`aria comporta che si possano definire leggi di resistenza a basso o alto numero di Reynolds.

L`equazione per la resistenza viscosa o lineare si riferisce a velocità relative alquanto basse in regime di assenza di turbolenza o di flusso quasi laminare: in tal caso si parla di drag force approssimativamente proporzionale al modulo della velocità ma opposto in direzione ossia F = -bv dove b è una costante che dipende dalla forma del proiettile e dalle proprietà del fluido attraversato. L`equazione che invece ci interessa più da vicino è quella che descrive il moto di un proiettile a velocità relative abbastanza elevate: essa è della forma F = ½ ρ v² C_d S dove ρ è la densità dell`aria, S l`area della sezione normale del proiettile,  C_d il coefficiente di drag, v la velocità del proiettile. Il coefficiente di drag C_d è una quantità adimensionale che esprime la resistenza dell`oggetto in moto relativo rispetto ad un fluido: esso dipende sia dal numero di Reynolds che da quello di Mach (quest`ultima data dal rapporto tra la velocità del proiettile nel fluido e quella del suono nel fluido stesso) quindi sia dalle caratteristiche fisiche del fluido che dalle condizioni di velocità relative. Ad un` analisi empirica più approfondita si ricava che il coefficiente di drag C<sub>d</sub> non ècostante ma varia in funzione della velocità (come d'altronde il coefficiente balistico che, essendo diretta filiazione di quello di drag, varia al variare della velocità), della direzione del flusso o dell`angolo d`attacco, della posizione del proiettile, della densità e della viscosità del fluido ed infine del profilo del proiettile.  A titolo d`esempio si riportano i grafici dei principali coefficienti di drag C_d, studiati a partire dalla fine del XIX° secolo.

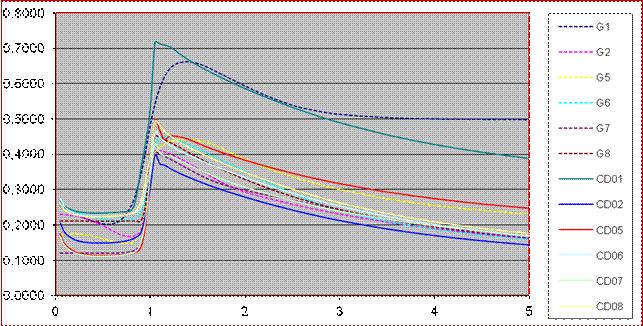
Fig.4

Il profilo aerodinamico dei proietti rappresenta, quindi, uno dei punti nodali dell`interazione proiettile –fluido.

Fig.5

L`immagine precedente, tratta dall`Handbook of ballistics – Exterior Ballistics di Carl Julius Kranz  precedente mostra un proiettile calibro 8 mm che fende l`aria creando vortici e turbolenze; notiamo dall`immagine successiva che l`evoluzione dei profili ha comportato l`adozione di un fondello del tipo boat–tail utile a minimizzare le turbolenze indotte dalla morfologia del fondello.

Fig.6

Un proiettile è un solido di rotazione o di rivoluzione ottenuto ruotando attorno ad un asse una regione piana sul cui piano giace l'asse stesso.

La nomenclatura di base dei profili dei proietti è basata su particolari grandezze: tali grandezze esprimono, mediante particolari equazioni, i parametri progettuali dei profili stessi.

Nel seguito L indicherà la lunghezza complessiva della punta o nose, R è il raggio alla sua base.  Le successive immagini definiscono le più comuni tipologie di profili della punta ossia conica, smussata sfericamente, biconica, ad ogiva tangente, ad ogiva tangente smussata sfericamente, ad ogiva secante, ellittica, parabolica, serie di potenze, serie di Haack, Von Karman.

 

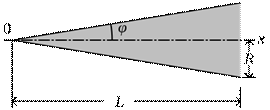
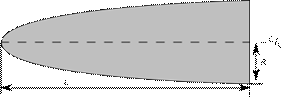
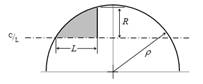
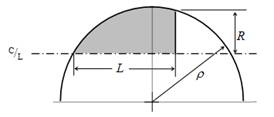
Fig.7

Un’ulteriore rappresentazione, derivabile dalla precedente è quella sviluppabile in funzione del calibro nominale del proiettile ossia C = 2R.

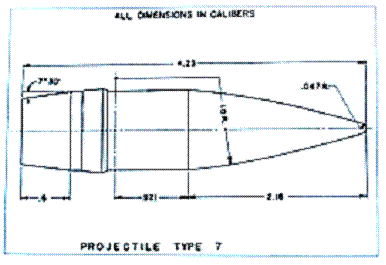
Fig.8

Per meglio comprendere le geometrie dei moderni proiettili vale la pena di rappresentarne i volumi delle parti principali ossia:

ogiva    

cilindro  

tronco di cono o boat tail o frustrum 

dove L_O, L_F ed L_C si riferiscono alla seguente figura

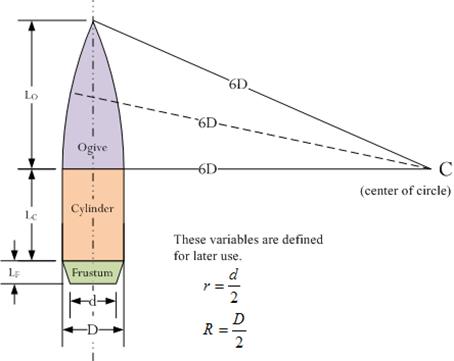
Fig.9

Tra tutti i profili rappresentati, quelli della serie di Haack non sono costruiti da figure geometriche, bensì matematicamente derivate al fine di offrire la minima resistenza. Le equazioni parametriche che definiscono la serie di Haack sono date da

                                                 

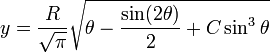
Nella figura seguente un esempio di profilo della serie di Haack

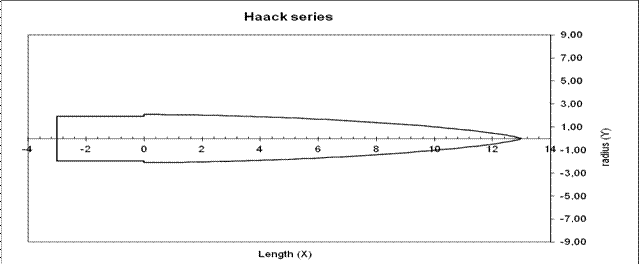
Fig.10

Wolfgang Haack lavorò durante la Seconda Guerra Mondiale, su di una formula analitica per profili aerodinamici che presentassero la minima resistenza all'aria.

Il suo lavoro Geschoßformen kleinsten Wellenwiderstandes (Bericht 139) venne pubblicato dalla Lilienthal-Gesellschaft nel 1941, ma secretato per tutto il periodo bellico.

Wolfgang Haack

In effetti uno dei problemi da affrontare in aerodinamica è il cambiamento di resistenza offerta dall’aria al variare della velocità: i profili di Haack risultano un compromesso tra i regimi supersonici, transonici ed infine subsonici, garantendo significative migliorie rispetto a canoniche forme di profili quali l’ogiva tangente o quella secante.

Infatti, generalmente, quando un proiettile decelera dalla velocità supersonica a quella transonica (ossia si trova nella regione compresa tra Mach 0,8 a Mach 1,2) il centro di pressione CP si sposta anteriormente compromettendo la stabilità aerodinamica in quanto vengono indotti sia movimenti di precessione che di tumbling: in ciò risiede la ragione per la quale l`attingimento del bersaglio dovrebbe essere garantito a velocità residuale supersonica.

Gli studi di Haack del 1941 e quelli di Sears del 1947, sembra portati avanti in maniera tra essi indipendente (cfr Haack, W. : Geschossformen kleinsten Wellenwiderstandes. Lilienthal- Gesellschaft für Luftfahrtforschung, Bericht 139, Teil 1, October 9-10, 1941, pp. 14-28. -Translations: Douglas Aircraft Co., Inc., Rep. 288, 1946; come anche Brown University Graduate Division of Applied Mathematics, Translation No. A9 -T -3, 1948. – Sears, W i l l i a m R. : On Projectiles of Minimum Wave Drag. Quarterly Appl. Math., vol. IV, no. 4, Jan. 1947, pp. 361-366.), si fondono nella definizione del corpo di Sears-Haack ossia di quella particolare forma che è alla base dell`ingegneria aerospaziale moderna.

Fig.11

Il corpo di Haack rappresenta un compromesso tra il volume e la forma di un proiettile in moto in un fluido.

Nel proprio incedere esso risulta soggetto alla minor wave drag vale a dire a quella componente di resistenza aerodinamica dovuta allo shock wave o per meglio dire a quel repentino (quasi discontinuo ed immediato) cambiamento delle caratteristiche (quali pressione, temperatura e densità) del fluido attraversato. Questi cambiamenti inducono la nascita di un fronte d’onda che viaggia a velocità superiori.

Tanto per intenderci riportiamo le immagini di una sequenza accelerativa:

 

 

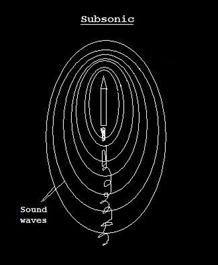
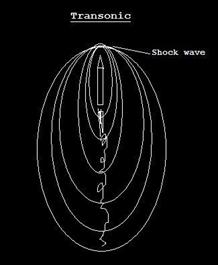
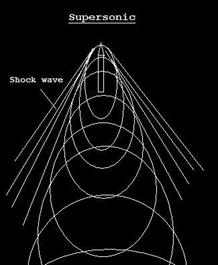
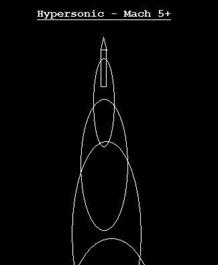
Fig.12

Nello studio citato Haack, applicando i canoni della teoria di Karman, approcciò in maniera originale il problema introducendo particolari relazioni funzionali (che legavano tra loro il meridiano descrittivo e la curvatura del profilo di un proiettile) nelle formule circostanziate della resistenza fluidodinamica,  semplificando queste ultime e imponendo formalismi variazionali su tre grandezze cardine individuate in sezione normale Q (o calibro K), lunghezza a e volume M: ricavò, quindi, regole generali reciprocamente vincolate dal fatto che date due tra le grandezze Q, a ed M la terza aveva stretti margini di variazione ossia dipendeva dalle precedenti.

Volendo rendere onore al genio di Haack non ci si può esimere dal tuffare, per un attimo, nel formalismo matematico del suo lavoro: infatti, Egli dedusse il meridiano più favorevole che descriveva il profilo

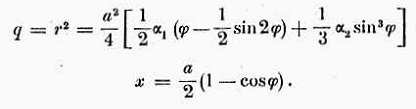
il volume M   

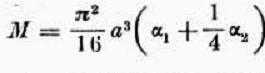
e la sezione normale Q

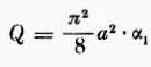
Queste relazioni comportavano che la resistenza aerodinamica più favorevole fosse espressa come

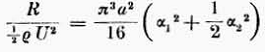
Seguivano le forme ottimali fornite dalle scelte di

calibro e lunghezza

volume e lunghezza

calibro e volume

così raccolte in un quadro sinottico

Passava, poi, ad introdurre un coefficiente adimensionale la cui applicazione comportava, in un particolare intervallo di velocità, l’evoluzione della forma dei proiettili in termini di punta ottimale a partire da un cilindro di dato calibro e volume (K-M).

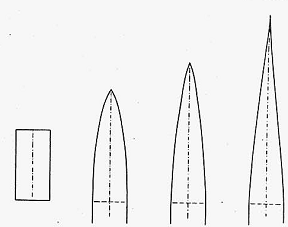
Infatti, come si osservava nelle seguente figura, il classico proiettile ogivale si avvicinava molto al profilo di quello ottimale del tipo M-L.

Un’ulteriore applicazione della semplificazione introdotta ab origine e computata mediante il coefficiente adimensionale implicava che dati volume e lunghezza (K-L) il profilo del proiettile diveniva più ottuso e la resistenza d’onda si riduceva (nb la figura numero 5, tra quelle in basso, rappresentava la punta limite).

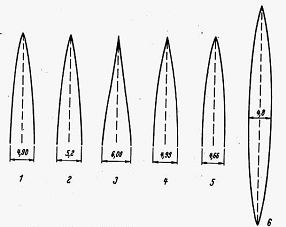
La forma numero 6 introduceva, quasi di soppiatto, un particolare proiettile (a fuso) ossia quello formato da una speculare parità di volume e lunghezza. Applicando al proiettile a fuso gli stessi meccanismi variazionali per la resistenza aerodinamica, opportunamente impostata data la particolare geometria,

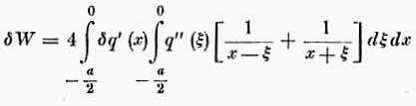
Haack ne calcolava il meridiano più favorevole  dati lunghezza, calibro e volume

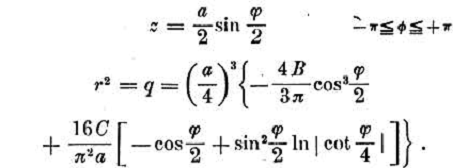
restituendo una particolare formula di resistenza

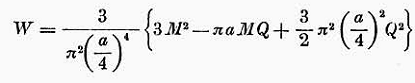
Anche in questo caso, come per i precedenti le punte erano ottuse ed al centro il raggio di curvatura tendeva a sparire. Passava, poi, nello specifico a calcolare la forma dei proiettili a fuso data una coppia di variabili scelte sulla terna di lunghezza, volume o calibro ottenendo, quindi,

per calibro e volume

per calibro e lunghezza

per lunghezza e volume

così, nuovamente, raccolte in un quadro sinottico

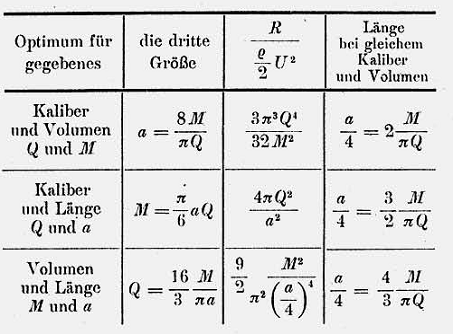
Ma passiamo ora dalla feconda astrusità dei calcoli a forme reali: infatti, nel 1940 vennero trovati proiettili di manifattura francese che, come Haack stesso segnala, avevano la meridiana tipica  dei proiettili del tipo K-M.

Fig.13

Se si comparava la seguente figura che rappresentava la migliore punta dato calibro e volume

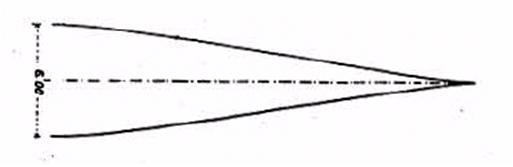
non potevano non notarsi similitudini che, impostati i calcoli al variare del calibro e della massa,  portavano a geometrie già ricavate nello studio: infatti il primo proiettile in alto di Fig.12 poteva ricavarsi dalle formule di Haack massimizzando il calibro.

Anche il primo proiettile di Fig.13

Fig.14

aveva un meridiano simile a quello K-M

L`asimmetria riscontrabile ictu oculi si spiegava con la circostanza che in una corrente supersonica si manifestava una perturbazione che si trovava all’interno di quello spazio per il quale passa il cono di Mach.

Partendo da quest`osservazione Haack accuratizzò le equazioni ottenendo, nel caso di Mach=2, la seguente forma di proiettile che coincideva con la geometria del proiettile francese.

Si palesava a questo punto una diretta correlazione tra velocità e forma del proiettile che sovvertiva le regole dell`integrazione di Karman e Moore e che induceva calcolarne il meridiano descrittivo e quindi a rappresentarlo asimmetrico in funzione del crescere della velocita`.

Si addiveniva alla costruzione di un proiettile a fuso privo di specialita` (cfr raggio di curvatura) e quasi simile a quello K-M: esso non minimizzava l`onda di resistenza ma al contempo godeva di ulteriori vantaggi.

Infatti il proiettile della figura seguente  

viaggiava da destra verso sinistra ad una velocita` di Mach=2 ed aveva un centro di gravita` spostato leggermente a sinistra.

La distribuzione di pressione lungo il meridiano cosi` come il campo di velocita` intorno al proiettile erano, quini, rappresentabili a questo modo:

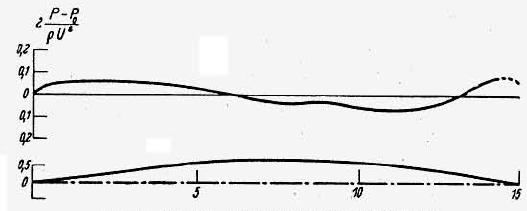
Si perveniva così al proiettile di Haack.

Riassumendo, l'efficienza del proiettile era quindi assicurata dal profilo che fendeva l'aria in un particolare modo allo scopo di ridurre l’onda di compressione: la punta doveva, in altre parole, aprirsi un varco nell’aria e penetrarla evitando, il più possibile, una compressione dei filetti fluidi.

Per concludere questa retrospettiva, dobbiamo però ricordare che Il problema, comunque, rimane.

Infatti, non esistono né possono esistere regole generali poiché la geometria dei proiettili varia in funzione del numero di Mach (essenzialmente il cono di shock wave  varia con la velocità del proiettile) e quindi della funzione specifica (artiglieria, armi corte/lunghe, sniping, caccia ecc)

Tirando le somme, quindi, vale la regola del compromesso ottimale in funzione della velocità media del proiettile.

Il geniale sforzo di Haack, però,  è considerato innanzitutto prodromico alle realizzazioni dei corpi con minor resistenza e si è concretizzato nello studio dei proiettili d’artiglieria, in taluni proiettili per applicazioni particolari e nell’avionica in generale.

Un particolare ringraziamento va al Dottore Mori per la paterna dedizione messa nella
traduzione, non facile, di questo lavoro dal tedesco.